线性范围的评估及数据处理方法
实验样本的基本要求和制备方法
基本要求
样本基质应与临床实验样本相似,但不可采用含有对测定方法具有明确干扰作用物质的样本,如溶血、脂血、黄疸或含有某些特定药物的样本。进行血清学标志物检测时,理想的样本为分析物浓度接近预期测定上限的混合人血清。
建立一种定量测定方法的线性范围时,需在预期测定范围内选择7-11个浓度水平。如将预期测定范围加宽至130%,在此范围内选择更多的浓度水平,然后依据实验结果逐渐减少数据点直至表现出线性关系,可发现最宽的线性范围。
当对标称线性参数进行验证时,需在已知线性范围内选择5-7个浓度水平。
无论是建立或验证线性范围,所选用的浓度水平应可覆盖整个预期测定范围并包括与临床有关的重要评价浓度,如最小测定浓度或线性范围的最低限、不同的医学决定水平、最大测定浓度或线性范围的高限等。
制备方法
不同浓度水平的样本可通过将高浓度样本与低浓度样本进行倍比稀释得到,注意在进行液体吸取时应选择精密度与准确性好的移液装置。制备时应将样本完全混合并避免蒸发或其他使样本变质的情况。每份样本的浓度与体积单位应统一。
如果高/低浓度血清的值未知,可将每种血清编码,用编码代表每个血清的相对浓度。对于等浓度间隔样本,可用连续整数(如1、2、3、4、5)代表连续样本。进行数据处理时可用样本号代替X值。表1和表2中描述的样本制备过程是按照等浓度间隔的设计进行的,每个浓度水平的样本量为1.00ml。
表1:11个浓度水平的样本制备
| 样本号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 低浓度血清(ml) | 1.00 | 0.90 | 0.80 | 0.70 | 0.60 | 0.50 |
| 高浓度血清(ml) | 0.00 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
| 样本号 | 7 | 8 | 9 | 10 | 11 | |
| 低浓度血清(ml) | 0.40 | 0.30 | 0.20 | 0.10 | 0.00 | |
| 高浓度血清(ml) | 0.60 | 0.70 | 0.80 | 0.90 | 1.00 |
表2:5个浓度水平的样本制备
| 样本号 | 1 | 2 | 3 | 4 | 5 |
| 低浓度血清(ml) | 1.00 | 0.75 | 0.50 | 0.25 | 0.00 |
| 高浓度血清(ml) | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 |
制备非等浓度间隔的样本时应明确各样本间的浓度关系,测定时可以这些样本间的相对浓度比值做为X值。
样本的特殊处理:在无法得到适用的人血清时,需对样本进行一些特殊处理以满足实验要求。这些处理过程包括稀释、加入添加物或透析、热处理等,无论进行何种处理均应以保持基质恒定为基本原则。在评价报告中应对所使用的稀释液、添加物、溶剂等的材料来源加以注明。
样本稀释液应选用由厂家推荐或经实验室证明可使用的产品,如可采用5%牛血清白蛋白或人白蛋白溶液。欲提高样本浓度时可在样本中添加分析物纯品。在添加物为溶液状态时,应注意添加液体对样本的稀释作用(小于10%)并注明所用溶剂。
实验过程
- 建立线性范围:需测定9-11个浓度水平,每个浓度水平重复测定3-4次。
- 验证标称线性参数:需测定4-6个浓度水平,每个浓度水平重复测定3-4次。
- 所有样本应在一次运行中或几次间隔很短的运行中随机测定,最好在一天之内完成。
数据处理
数据记录
可参考下表进行数据记录,也可采用其它形式进行记录,但应注意保留原始数据。
| 项目: | 样品: | ||||
| 仪器: | 试剂/批号: | 校准品/批号: | |||
| 操作者: | 审核者: | 测定日期: | |||
| 样本号 | 测定1 | 测定2 | 测定3 | 测定4 | 均值 |
| 1 | |||||
| 2 | |||||
数据可用性检查
可通过绘制散点图对测定数据的可用性进行初步检查。以样本号或样本浓度为X轴,以测定结果为Y轴做图,在图上标出针对每个样本的测定值及每个浓度水平的测定均值,手工或用计算机做图将均值点相连,观察数据点与直线间的偏差,如偏差过大,表明数据组存在明显非线性,需要对测定过程进行检查,排除因操作错误所至误差,并对样本进行重新测定。如图形与直线接近,表明可对数据组继续进行统计分析。
剔除离群值
离群值可由散点图初步判断,标准中建议采用格拉布斯(GRUBBS)法进行离群值检验。检验步骤如下:
- 1. 每组数据中有4个测定结果,分别记为 y1,y2,y3,y4。
- 2. 将4个测定值按大小顺序排列,最大值记为max,最小值记为 min;
- 3. 由4个测定值计算均值y和标准差S:
y=(y1+y2+y3+y4)/4;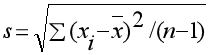
- 4. 根据可疑值 max或 min分别按下式计算统计量t:
t1 = (max-)/S,t2 = (min-)/S; - 5. 根据给定的显著性水平a和重复测定次数查表得临界值,如t值大于临界值,则相应的可疑值为离群值。
进行多项回归分析
对数据组进行多项回归分析,得到一级、二级与三级多项式。一级多项式为直线,二级多项式表示上升曲线或下降曲线,三级多项式表示S形曲线(在测量范围两端具有明显的非线性)。多项式方程如下:
| 级数 | 多项式 | 回归自由度(Rdf) |
|---|---|---|
| 一级 | Y = b0 + b1X | 2 |
| 二级 | Y = b0 + b1X + b2X2 | 3 |
| 三级 | Y = b0 + b1X + b2X2 + b3X3 | 4 |
对回归方程进行线性检验
多元回归方程中以bi表示的系数为回归系数。在二级与三级方程中,b2与b3为非线性系数。对回归方程进行线性检验就是对每个非线性系数作t检验,判断回归系数与零是否有显著性差异。b0与b1不反映非线性,故不需对其进行检验。对b2与b3的检验方法如下:
计算统计量t,计算公式为:
t = bi/ SEi
式中SEi 为每个非线性系数的斜率标准误,计算公式为:
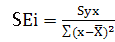 ;
;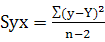 ;
;
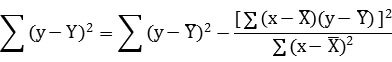 ;
;
其中,Y为回归方程预测值,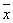 与
与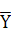 与为测定均值。
与为测定均值。
由公式df = L*R-Rdf 计算自由度,L为样本数,R为每个样本的测定次数,Rdf为回归自由度,即回归方程中系数(包括b0)的个数。如测定5样本,每个样本重复测定4次,则对测定数据进行回归分析后其三级多项式中L=5,R=4,Rdf=4,df=5*4-4=16。在t值表中寻找t界值(双边检验,α=0.05),将计算出的t值与界值比较,如p>0.05,表示非线性系数与零无显著性差异,数据组被认为具线性,此时可对数据组进行精密度检验,具体方法见后。当精密度符合线性判断要求时,数据分析可结束。如p<0.05,表示此非线性系数具有统计学显著性,数据组为非线性,此时应进行临床标准的线性与非线性检验。
临床标准的线性与非线性检验
上述多项式回归分析主要是利用统计学方法进行线性判断,统计学标准的线性可称为一阶线性,对数据组的要求很高。对于在临床实验室中使用的测定方法,在其临床应用实践中允许有一定的非线性误差,此时通过对统计学标准的非线性作程度判断,可得到临床标准的线性,即二阶线性。
临床标准的线性检验中使用了两个统计量,ADL(偏离直线平均差异,average deviation from linearity)与PctBnd(百分区界 ,percent bound) ,对于大多数分析物PctBnd取5%。如ADL小于所要求的临界判断值,则可认为数据组具有临床可接受的线性,所拟合出的最适非线性多项式无临床意义。
ADL值的计算:
ADL表示最优拟合曲线与直线的平均差异,其计算公式如下:
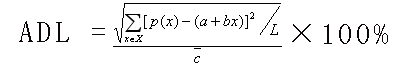
式中p(x)表示最优拟合二阶或三阶方程的拟合值,a+bx表示拟合一阶方程的拟合值,L表示样本数,c表示总平均浓度(全部测量数据的平均值)。
将ADL与临界值比较
一般设定ADL小于5%为临床允许误差,即取PctBnd为5%,通过查表(见附表A与B)得到ADL临界值。如ADL小于临界值,可认为多项式具有临床可接受的非线性,为二阶线性。如ADL大于临界值,则为临床不可接受的非线性。
对数据组进行精密度检验
测量数据的精密度可直接影响多项式回归分析的结果,为提高统计功效,需对数据组进行精密度检验。
计算最优拟合方程的回归标准误(σ)
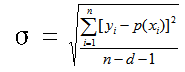
式中yi表示各个测量值,p(xi)表示最优拟合方程的拟合值,n表示样本数乘以重复次数(L x R),d表示最优拟合方程的阶数。
计算不精密度
用最优拟合方程的回归标准误(σ)与总平均浓度(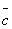 )的百分比代表不精密度。
)的百分比代表不精密度。
数据组的不精密度检验
跟据以下公式进行判断:
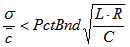
式中σ表示最优拟合方程的回归标准误,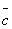 表示总平均浓度,L表示样本数,R表示重复测量的次数,C表示常数(附表C),PctBnd:取5%。
表示总平均浓度,L表示样本数,R表示重复测量的次数,C表示常数(附表C),PctBnd:取5%。
不精密度满足判断式时, 说明数据的精密度好可作线性评价。反之则表示数据的精密度差,不能作线性评价。当PctBnd取5%时, 尚可通过查不精密度和临界值表判断数据是否精密 (附表A和B), 如此时不精密度对应的临界值显示P, 表明测量数据的精密度不符合作线性判断的要求。
结果报告
线性范围报告的具体格式不要求,但至少应包括以下几方面:
进行线性评价的实验室或生产厂家名称。
被评价的方法或试剂名称,批号。
测定项目。
线性范围(如为二阶线性应包括临床允许误差)。
如可能应标出测定项目的医学决定水平及在此水平处的临床允许误差。
附录:
表A:不精密度和ADL的临界值(PctBnd=5%,d=1或2阶)
| σ/% | L*R=10 | L*R=12 | L*R=14 | L*R=16 | L*R=18 | L*R=20 |
| 1 | 5.5 | 5.5 | 5.4 | 5.4 | 5.4 | 5.4 |
| 2 | 6.1 | 6.0 | 5.9 | 5.8 | 5.8 | 5.7 |
| 3 | 6.6 | 6.4 | 6.3 | 6.3 | 6.2 | 6.1 |
| 4 | 7.1 | 6.9 | 6.8 | 6.7 | 6.6 | 6.5 |
| 5 | 6.6 | 7.4 | 7.2 | 7.1 | 7.0 | 6.9 |
| 6 | 8.2 | 7.9 | 7.7 | 7.5 | 7.4 | 7.2 |
| 7 | 8.7(P) | 8.4(P) | 8.1 | 7.9 | 7.8 | 7.6 |
| 8 | P | P | 8.6(P) | 8.3(P) | 8.1 | 8.0 |
| 9 | P | P | P | P | 8.5(P) | 8.3(P) |
| >9 | P | P | P | P | P | P |
L*R:样本数*重复测量的次数
表B:不精密度和ADL的临界值(PctBnd=5%,d=3阶)
| σ/% | L*R=10 | L*R=12 | L*R=14 | L*R=16 | L*R=18 | L*R=20 |
| 1 | 5.5 | 5.5 | 5.4 | 5.4 | 5.4 | 5.4 |
| 2 | 6.1 | 6.0 | 5.9 | 5.9 | 5.8 | 5.8 |
| 3 | 6.7 | 6.5 | 6.4 | 6.3 | 6.2 | 6.2 |
| 4 | 7.2 | 7.0 | 6.9 | 6.8 | 6.7 | 6.6 |
| 5 | 7.8 | 7.6 | 7.4 | 7.2 | 7.1 | 7.0 |
| 6 | 8.4 | 8.1 | 7.9 | 7.7 | 7.5 | 7.4 |
| 7 | 9.0(P) | 8.7(P) | 8.4 | 8.2 | 8.0 | 7.8 |
| 8 | P | P | 8.9(P) | 8.6(P) | 8.4 | 8.2 |
| 9 | P | P | P | P | 8.9(P) | 8.7(P) |
| >9 | P | P | P | P | P | P |
L*R:样本数*重复测量的次数
表C:不精密度界值的常数
| 最优拟合方程的阶数 | 精密度界值的常数(C) |
| 一阶或二阶 | 6.3 |
| 三阶 | 6.5 |

相关产品



 苏公网安备32011202001302
苏公网安备32011202001302